Transient dynamics

A transient phase is the pattern of change as a system moves from one equilibrium state to another. The transition phase is often described as, or assumed to be, abrupt and dramatic. But transition phases in the real world play out over a variety of timescales depending on the system size, the frequency of drivers or stressors and the type of transition. A system may exist almost continuously in a transient state if there is frequent disturbance. A better understanding of how long transitions take and what determines the length of transition time is crucial for making appropriate management interventions. The figure below shows that, at least in mathematical models, the pattern of transition depends strongly on whether the system is a fast or slow responder to a driver irrespective of the type of dynamic system. Importantly, slowly responding systems always exhibit a gradual shift in ecosystem state through time. Three big questions are how would we know that a regional social-ecological system has passed a tipping point - how long will it take to reach a new state - and what will the new state look like?

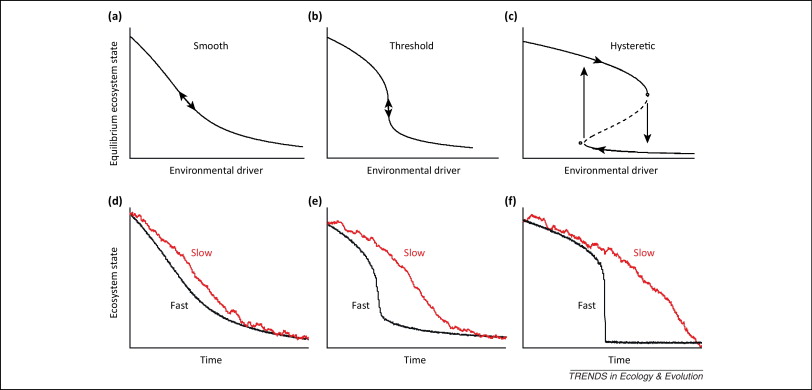
Figure: The response of a dynamic system (at equilibrium) to slowly changing conditions or environmental drivers can be (a) smooth, (b) threshold-dependent or (c) threshold-dependent through a critical transition/fold bifurcation between two alternate stable states. Panels (d–f) show simulations of system responses under each of these dynamics to an escalating driver. The two curves in each panel represent the cases of fast (black line) and slow (red ine) responding systems. The simulations show that fast-responding systems exhibit trajectories that vary from gradual (d) through rapid (e) to abrupt (f) changes depending on the system dynamics, but slowly responding systems always exhibit a gradual shift in ecosystem state through time even after a steep threshold has been transgressed (Hughes et al., 2013).