- Home
- » Complexity Theory
- » Thresholds and tipping points
Thresholds and Tipping Points
A threshold is a point in a condition or process that once passed triggers some kind of change. Your savings in a bank account reach a threshold point that triggers you to go out and buy a car! In complex systems, thresholds are a major reason for nonlinear behaviour. A tipping point has a similar meaning but is more related to systems: signifying a critical point after which the system shifts radically and potentially irreversibly into a different equilibrium state.
The figure below shows linear and nonlinear change in the response of a system in an equilibrium state to changing conditions, like water quality responding to changes in nutrient loading. The first type of response (a) is linear, incremental and smooth following the increasing conditions , and may be reversible along the same trajectory if the driver of the conditions is decreased or restored to previous levels. The second type (b) shows threshold-dependent, nonlinear behaviour where the system moves from one state to another. In reality, this may also be quite easy to reverse. The third type (c) also shows threshold-dependent behaviour, but a special type known as a critical transition or catstrophic fold bifurcation where the upper line state reaches a tipping point at F2, before dropping to the lower line state. As the names suggest, these are threshold-dependent changes associated with abrupt, surprising and irreversible shifts in the form and function of a system. The term regime shift is often used to describe this kind of major shift. Fold bifurcation is the mathematical formulation whereby there are actually three equilibrium states, but where one is extremely unstable (the dotted line). Systems that come close to this unstable state rapidly move to one of the other stable states as shown by the arrows. There are two ecosystem states for a wide range of conditions between the two threshold positions F1 and F2 where moving back from the lower line state to the upper line state means changing the conditions at least as far as F1.
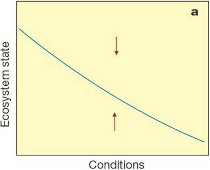
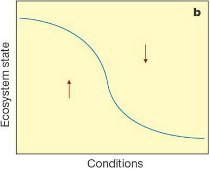
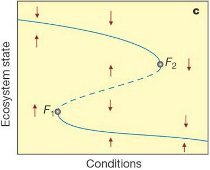
Figure: System change in response to a range of conditions a) linear, b) threshold-dependent nonlinear, c) threshold-dependent critical transition showing a fold bifucatiion relationship (Scheffer et al 2001).
Scientists have observed tipping points in many real world systems, such as marine fisheries, lake water quality and the world's climate. Identifying tipping points that we have already crossed in real world systems and working out where they may be in the future has become a major scientiifc endeavour. Anticipating critical transitions in social-ecological systems is arguably even more important for sustainable development and ecosystem management, where for the sake of people's livelihoods and social wellbeing we have to avoid catastrophic changes before they creep up on us and take us by surprise.


 中文版本
中文版本